BPTT法は、時刻 
から t までネットワークの計算を行いながら、入出
力と結合荷重を保持しておき、その後 t から まで誤差の計算、およ
び結合荷重の更新を行う方法である。そのため、この際用いる出力の教師信号は
時刻 t におけるもののみで、時刻 から t までの間のものは用いない。この方法は離散時刻の場合には、RNNをフィードフォワードの階層型NNとみなしてBP法を適用することと等価である。
ここで時刻 における入力 
と時刻 t のみにおける教
師信号 
を与えたとき、時刻 t における出力ユニット 
の出力 
が教師信号 になるような学習法を考察する。
ここで、ネットワーク全体の2乗誤差関数を
とする。ただし、
である。
この誤差関数 E を極小化するような学習則を考えたい。
ここでは各時刻 
ごとの結合荷重 
は時刻 には依
存しない定数 
であるとする。
誤差関数 E を結合荷重 
で偏微分すると、
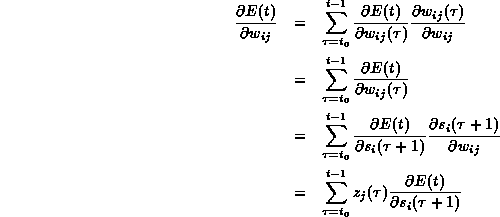
となる。
よって、 
を計算するためには、 
を求めなければならない。
そのため、出力ユニット（ 
）・隠れユニット（ 
）の2つの場合を分けて考える。
まず、 、すなわち出力ユニットへの結合荷重に対しては、
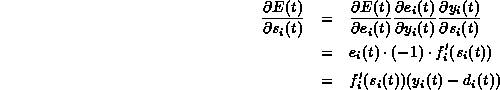
次に、 、すなわち隠れユニットへの結合荷重に対しては、
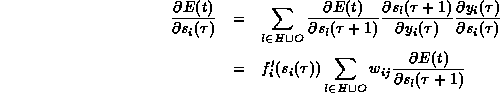
となる。
従ってこれらから、 を再帰的に求めることができる。
ここで、
とおけば、
と整理される。 よって、結合荷重の更新は
とすればよい。ここで 
は学習率である。
前述のようにBPTT法では学習を行う際、入出力や結合荷重を保持しなければならない。よって考慮する期間が長くなるほど、計算量と必要なメモリーの量が増えていく。このような理由から、BPTT法では無限に続く波形を学習することは不可能である。 実際に学習を行う場合には、過去の入出力や結合荷重をすべて保持せず、あらか じめ定められた h 時点前までのデータのみを保持し、それ以前のデータは保 持しないで、近似するという打ち切り型通時的逆伝播（truncated BPTT）法が提 案されている（Williams and Zipser,1989;1995）。この方法を用いることで計 算量と必要なメモリーの節約が可能である。しかし、近似に必要な h が大きくなれば同じことであり、上に書いたような問題に対しての根本的解決とはならない。