対象とする問題

まず以下に簡単に、FSM,FMM,SMの定義を示す。

• Finite state machine
  FSMは有限な数の入出力記号を処理し、有限な数の状態を持つ。出力はそれに対応する入力によって定義される。 形式的には、

  定義1.　FSMは の6文字組 みで定義される。ここで Q は状態の有限集合； は入力記号 の有限集合； は出力記号の有限集合； は遷移関数； は出力関数； は初期状態である。

  ここでは、入出力記号は である。

  最も少ない状態数で求める入出力の動作を行うことのできるとき、そのFSMは最 小であるという。ここでのFSMはすべて最小のものである。各々のFSMを 特徴付ける有効な尺度はdepthである。FSMの初期状態からすべての状態 に達することのできる最小の数 d があるとき、これをdepthという。

• Finite memory machine
  FSM M は、入力order n ,出力order m のn,m が最小の整数であるとき、 すなわち M の現在の状態が最後の n 個の入力、および m 個の出力によって一意に定まるとき、Finite memory machine(FMM)であるという。 また、ある任意のFSMが与えられたとき、それがFMMであるか、またそのorderはなにかを実際に計算するアルゴリズムが存在する(Kohavi,1978)。

• Sequential machines
  順序機械は論理回路と遅延素子からなり、現在の状態が最後のn個の入力、およびm個の出力によって一意に定まるようなものである。これは論理関数の形で表現することができる。

• 問題について
  SM（sequential machine）は、論理回路と遅延素子からなり、入力・出力の過 去の n,m 個の値を保持している。そして、それによって次のステップの出力が決まるというものである。このSMは、FMMと呼ばれる特殊なタイプのFSMによって表すことができる。このときSMによってはFMMの状態数はかなり大きなものになる。ここではRNNを用いて、このような、従来の研究に比べてサイズの大きなFMMの学習を行う。

  一般に、FMMに実装された論理関数が単純で、最小のorderと小さいdepthを持っているなら、それを学習させることはやさしい。FMMを学習するという問題は、状態の割り当ての問題が無いため、一般的なFSMの学習より単純である。学習すべき唯一の問題は実装された論理関数である。ゆえに、論理関数が複雑になればなるほど、学習は難しくなるといえる。また、トレーニングセットを小さくするためには、depthも小さく抑えねばならない。さらに、orderはdepthと論理関数の複雑さの両方と関係しており、同様に小さく抑えねばならない。 その結果、上記を考慮して、学習の対象とするFMMは、状態数と論理回路を表す論理関数、入出力のorder、およびdepthの異なる２種類を選んだ。以下で、それらについて具体的に示す。

  最初の１つは、512状態と次式で表される比較的単純な論理関数を持っている。

  

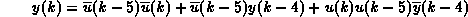
  ここで、 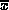は x の否定をあらわす。また、 u(k),y(k) はそ れぞれ時間ステップ k における入力、出力である。また入力のorderは5、出力のorderは4、depthは9である。

  もう１つのものは、256状態を持ち、次のようなより複雑な論理関数を持つ。

  

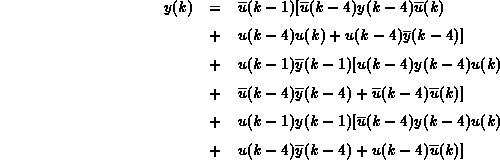
  入力のorder、出力のorderはともに4、depthは9である。