接続係数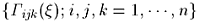 は、点p
ごとに定まる n3 個の実数で、接続を導入することで見えてくる多様体の「曲がり具合」を示していると考えることができます。 は、点p
ごとに定まる n3 個の実数で、接続を導入することで見えてくる多様体の「曲がり具合」を示していると考えることができます。
一般にアファイン接続は無数に存在し、アファィン接続の接続係数は無数に存在します。
平坦性
接続係数が0のとき、つまり多様体が「曲がっていない」とき、平坦な接続だといいます。
無数のアフィン接続が存在する中で、統計的モデルに対して平坦となるような接続を選ぶことが、統計的性質を幾何学的に取り扱う上で重要となります。
一般に、計量と接続を外から与えてやることで、多様体の構造が決まり、平坦性が定義できるようになります。ある接続においては平坦となっても、別の接続では平坦にはなりません。接続とはそのようなものであることに留意しておいてください。
共変微分
これは、基底ベクトル∂j を∂i 方向にうごかしたときに、∂j がどのくらい変わっていくかというベクトルを意味します。 |