| ある事象xが発生する確率を与える関数p(x)を確率分布とよびます。
確率分布p(x)>0がn個の実数パラメタの組ξ=(ξ1,ξ2,... ,ξn)によって与えられるとき、
p(x,ξ)と書きます。 ξのあらゆる組み合わせを考えて、p(x,ξ)全体の集合、
S = { p(x,ξ) }
を統計的モデルとよび、このSをn次元の空間(n次元多様体)として扱います。
統計的モデルには様々な種類があります。以下にその例を挙げます。
1.正規分布 ( x∈R, ξ=[μ,σ], -∞<μ<∞, 0<σ<∞ )
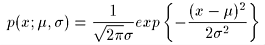 (1) (1)
|
2.ポアソン分布 ( x∈{ 0, 1, 2,…}, ξ>0 )
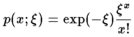 (2) (2)
|
3.離散分布 ( x∈{ x1, x2, x3, ..., xn }, ξ=[ξ1,…, ξn],
ξi>0,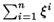 <1
) <1
)
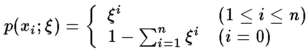 (3) (3)
|
パラメタξは1つの確率分布の性質を表します。 統計的モデルは、可能な全てのξによる確率分布の集合です。
ξが変化すると確率分布がどのように変化するかという性質が、確率的モデルの性質となり、
これを幾何学的に考えるのが情報幾何です。 |